Here was the original problem:
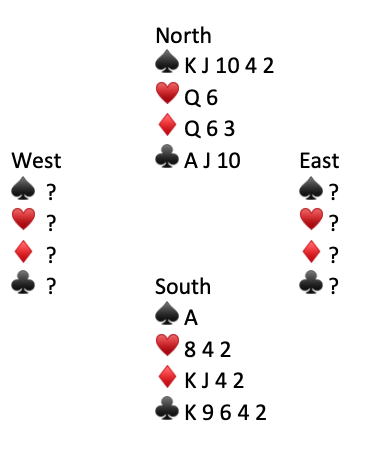
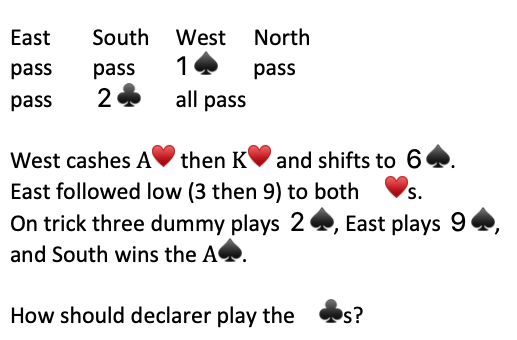
Solution–
The principle of vacant spaces says that the probability that an opponent holds a particular card is proportional to the number of vacant spaces remaining in their respective hands. In this case we know that West started with at least five ♠️s, two ♥️, and probably the A♦️ (for his/her opening bid). So West has five “vacant spaces”. East is known to have at least one ♠️ and two ♥️s–hence ten “vacant spaces”. Bottom line–East is twice as likely to have Q♣️.
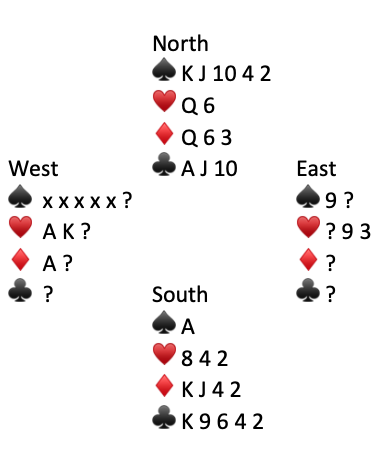
Lead small to A♣️ then return J♣️ for a finesse. If J♣️ wins you will want to try the K♠️ while you are still in dummy. Otherwise you are likely to lose a third ♥️. If East follows to K♠️ you can discard your losing ♥️ and get back to trumps. If East ruffs K♠️ then over ruff and trump your last ♥️ with 10♣️. Here was the entire deal:
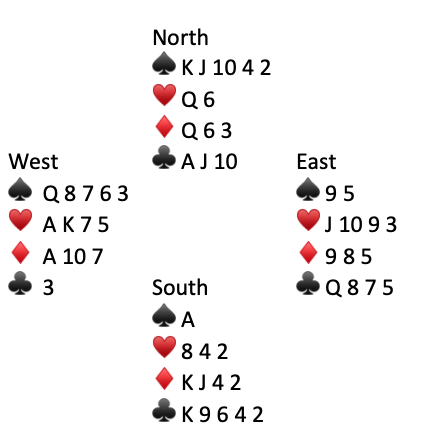
At our table South played for the drop in ♣️s and ended up winning only 9 tricks for a 47% matchpoint score. Making ten tricks in a 2♣️ contract would have scored a 63% board. The principle of vacant spaces should be an automatic choice in these situations.
[For more bridge quizzes click on Bridge Index page.]

